现代神经网络架构¶

本章介绍的神经网络是将人类直觉和相关数学见解结合后，经过大量研究试错后的结晶。将按照时间顺序介绍这些模型，在追寻历史的脉络的同时，帮助培养对该领域发展的直觉。这将有助于研究开发自己的架构。

例如，本章介绍的批量规范化（batch normalization）和残差网络（ResNet）为设计和训练深度神经网络提供了重要思想指导。

1. AlexNet¶

本质上是一个更深更大的LeNet，做的改进有：

丢弃法
ReLu
MaxPooling

通过CNN学习图像特征（深度学习神经网络），再由softmax回归分类。

由于当时GPU运算性能不够，所以第一层卷积层步幅为4。输出通道数大大多于LeNet。更多细节：

激活函数为ReLu
隐藏全连接层后加入丢弃层
数据增强

复杂度：

代码实现：

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

构造一个高宽都为224的单通道数据为输入，得到每层输出shape：

2. VGG¶

2.1 VGG块¶

使用 $3\times 3$ 卷积，padding = 1，n个卷积层（n是超参数），m通道
加上一个 $2\times 2$ 最大池化层，stride = 2

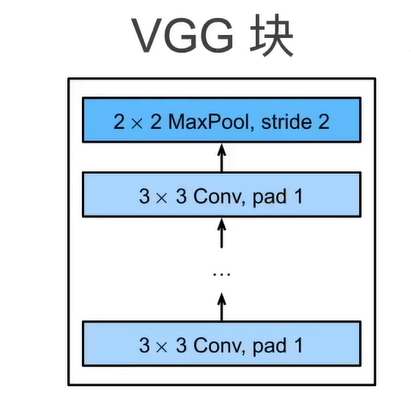
why $3\times 3$ : 研究发现深但窄效果会更好。

2.2 VGG架构¶

多个VGG块连接后后接全连接层得到VGG架构，不同次数的重复块得到不同的架构。

2.3 实现¶

定义VGG块：

import torch
from torch import nn
from d2l import torch as d2l

#卷积层的数量num_convs、输入通道的数量in_channels 和输出通道的数量out_channels.
def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        #更新
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

实现VGG-11：

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

同样是高宽都为244的单通道数据为输入，观察每层输出shape为：

其训练速度比AlexNet慢，但精度高于AlexNet。

3. NiN¶

全连接层的问题：

带来过拟合
所需参数过多

3.1 NiN块¶

一个自定义的卷积层后跟两个 $1\times 1$ 卷积层，这两个 $1\times 1$ 卷积层步幅为1，无填充，输出形状和卷积层输出一样，起到全连接层的作用，对图片的每个像素增加了非线性性

3.2 NiN架构¶

最后的一个层使用全局平均池化层替代VGG和AlexNet中的全连接层，更少的参数个数，不容易过拟合。

3.3 实现¶

nin块：

import torch
from torch import nn
from d2l import torch as d2l


def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        #自定义卷积层
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        #1x1卷积层+激活层，通道数不改变
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

nin模型：

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10，输出等于标签类别数
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    #取10个通道中每个矩阵的平均，size变为[1,10,1,1]
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

同样创建一个224 x 224的数据样本来查看每个块的输出形状：

4. GoogLeNet¶

GoogLeNet吸收了NiN中串联网络的思想，并在此基础上做了改进。提出该网络的论文解决了什么样大小的卷积核最合适的问题。

4.1 Inception块¶

在GoogLeNet中，基本的卷积块被称为Inception块 ：

Inception块由四条并行路径组成，都使用合适的填充来使输入与输出的高和宽一致。
四个路径从不同层面抽取信息，最后我们将每条线路的输出在通道维度上连结，并构成Inception块的输出。（白色层用于变换通道数，蓝色层用于提取信息）
在Inception块中，通常调整的超参数是每条线路的输出通道数。
与单3 x 3或5 x 5卷积层比，Inception块有更少的参数个数和计算复杂度

Inception之后有各种变种，这里介绍的是初始版本。

4.2 GoogLeNet¶

GoogLeNet一共使用9个Inception块和全局平均汇聚层的堆叠来生成其估计值，是第一个达到上百层的网络。
Inception块之间的最大汇聚层可降低维度

段1 & 2：

GoogLeNet 降宽更为缓和。

段3：

段4&5：

4.3 Inception V3¶

4.4 实现¶

实现见网站，没有什么好讲的，就根据模型来。

5. 批量归一化¶

数据从最底层往上传递（正向），而梯度从最顶层往下算（反向传输），权重从顶至下更新，梯度往下传输时越来越小，所以下面收敛更慢。而当底部层变化，所有层都要跟着变化，导致收敛变慢

为避免在学习底部层时避免顶部层变化，我们运用 批量归一化 来解决这个问题。

将输入的小批量样本里的均值和方差求出来（在方差估计值中添加一个小的常量 $\epsilon > 0$，以确保我们永远不会尝试除以零）：

应用标准化，使得生成的小批量输出的平均值为0和单位方差为1：

$\gamma,\beta$是需要和其它模型参数一起学习的参数，分别叫做拉伸参数scale和偏移参数shift。

这加快了收敛速度，但一般不改变模型精度。

5.1 批量归一化层¶

批量归一化是起一个线性作用。

该层中可学习的参数为 $\gamma$ 和 $\beta$
它直接作用在全连接层和卷积层输出上，激活函数连在它后面
作用在全连接层和卷积层输入上
对于全连接层，作用在特征维；把每一个特征对应的列设均值和方差
对于卷积层，作用在通道维；假设一个像素通道为100维，那么这100维的向量就是这个像素的特征，每个像素看作一个样本。

批量归一化是在做什么？

通过在每个小批量里加入噪音来控制模型复杂度，$\sigma_B$ 和 $\mu_B$ 是随机选取的小批量样本的方差和均值，可看作噪音：

5.2 实现¶

数据计算：

import torch
from torch import nn
from d2l import torch as d2l

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        #2维是全连接层 4维是卷积层
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差 momentum一般为0.9
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

创建一个正确的 BatchNorm 图层：

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

除了使用我们刚刚定义的BatchNorm，我们也可以直接使用深度学习框架中定义的BatchNorm：

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
    nn.Linear(84, 10))

通常高级API变体运行速度快得多，因为它的代码已编译为C++或CUDA，而我们的自定义代码由Python实现。

6. ResNet¶

假设 $f^*$ 是最佳训练函数，$F$ 是一类特定的神经网络架构。如果 $f^* \in F$，那么可以通过训练神经网络得到最佳选择。但大多数时候 $f^*$ 不在架构中，这时我们通过构造一个更强大的 $F$ 架构，使其更接近最优解 $f^*$。

在面对非嵌套函数 non-nested function 时，架构更复杂反而可能远离最优解。例如 $F_6$ 较 $F_3$ 更加复杂，却离最优解更远。
nested-function则没有这种烦恼，因为每一个更复杂的模型都包含了前面的模型。

6.1 残差块¶

由此，我们需要构造 nested-function。

当 $f(x)$ 无效时，输出就是输入 x（也就是更小架构的输出）。这使得很深的网络更加容易训练。

在ResNet中，残差块结构为：

当use_1x1conv=False时，应用ReLU非线性函数之前，将输入添加到输出。另一种是当use_1x1conv=True时，添加通过1×1卷积调整通道和分辨率。

代码：

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        #定义第一个3 x 3卷积层
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        #第二个
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        #batch_norm层
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X  #f(x) + x
        return F.relu(Y)

6.2 ResNet模型¶

ResNet的前两层跟之前介绍的GoogLeNet中的一样：在输出通道数为64、步幅为2的7×7卷积层后，接步幅为2的3×3的最大汇聚层。不同之处在于ResNet每个卷积层后增加了批量规范化层。

GoogLeNet在后面接了4个由Inception块组成的模块。 ResNet则使用4个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。

6.3 实现¶

#初始块
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            #每部分残差块的第一块stride=2 高宽减半；第一部分残差块除外
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk

#接入残差块，每部分num_residuals = 2
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

6.4 ResNet 梯度计算¶

为什么 ResNet 可以设计得很深却不会发生梯度消失，原因如下： $$ y = f(x)\ w = w - \eta \frac{\partial y}{\partial w}\ 假设y是底层的一个输出，我们需要使得\frac{\partial y}{\partial w}不会很小\ y\prime = g(f(x))是y经过残差块之后的输出\ \frac{\partial y\prime}{\partial w} = \frac{\partial y\prime}{\partial y} \frac{\partial y}{\partial w} = \frac{\partial g(y)}{\partial y}\frac{\partial y}{\partial w} \ 假如\frac{\partial g(y)}{\partial y}很小，就会使得\frac{\partial y\prime}{\partial w}变小\ y\prime \prime = f(x) + g(f(x)) = y + y\prime\ \frac{\partial y\prime \prime}{\partial w} = \frac{\partial y}{\partial w} + \frac{\partial y\prime}{\partial w}\ 即使 \frac{\partial y\prime}{\partial w}小也没事，\frac{\partial y}{\partial w}会把结果拉回来 $$ 注：此处 $y\prime$ ，$y\prime \prime$ 和 $y$ 之间没有求导关系，表示从下往上残差块之间的输出。因为ResNet有跳转，所以直接可以获取底层的梯度并保证其不会太小。